蒙特卡洛方法(英语:Monte Carlo method),也称统计模拟方法,是1940年代中期由于科学技术的发展和电子计算机的发明,而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
20世纪40年代,在冯·诺伊曼,斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡洛方法。因为乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名,而蒙特卡罗方法正是以概率为基础的方法。
与它对应的是确定性算法。
蒙特卡洛方法在金融工程学,宏观经济学,生物医学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。
基本思想
把所求解的问题转换为某种随机分布的特征数,例如随机事件出现的概率,或者随机变量的期望值。通过随机抽样的方法,以随机事件出现的频率估计其概率,或者一抽样的数字特征估算随机变量的数学特征,并将其作为问题的解。
应用
求解圆周率
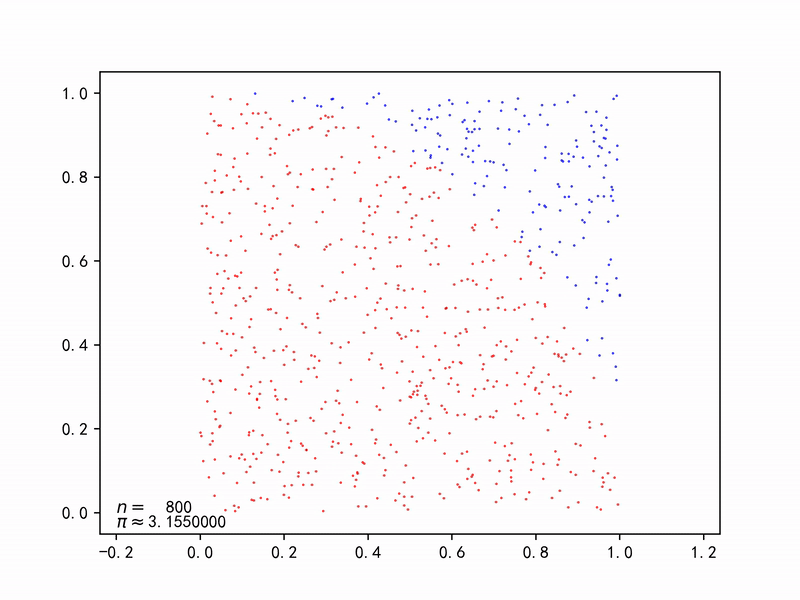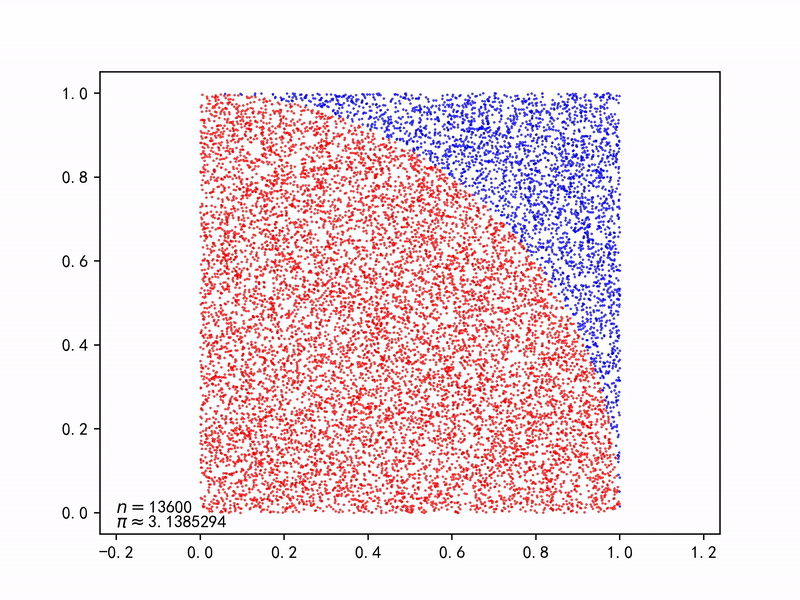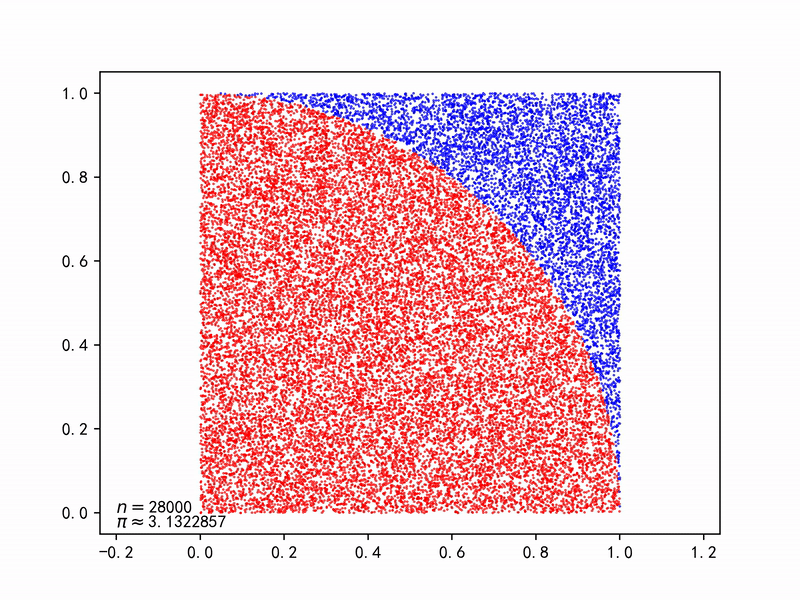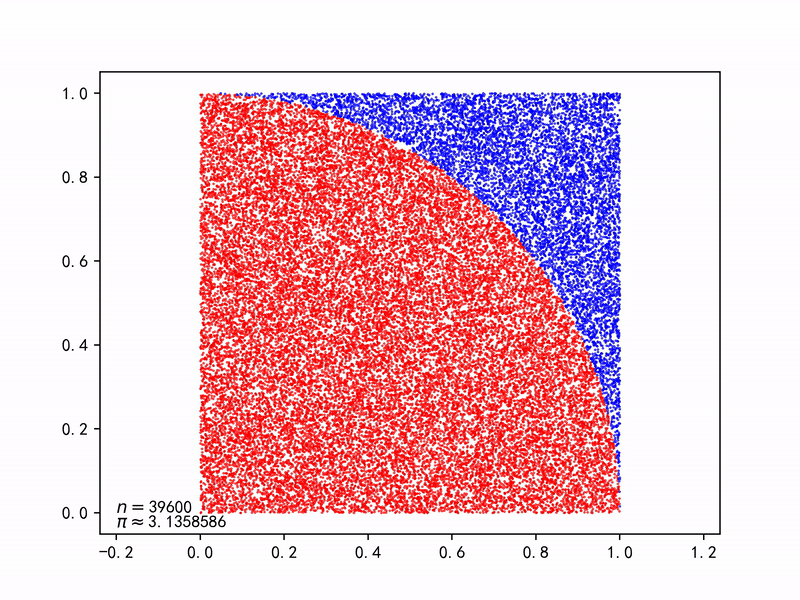
圆形的面积为$A_s=\pi r^2$,正方形的面积为$A_q=(2r)^2$, 则产生一对随机数$(x_i, y_i)$落在圆内的概率为: $$ p=\frac{A_s}{A_q}=\frac{\pi r^2}{(2r)^2}=\frac{\pi}{4} $$ 只要不断产生一对对随机数$(x_i, y_i)$,由于大数法则(Law of large numbers),能以随机事件(落在圆内)出现的频率估计其概率,再求解$\pi$。
代码 Gist | Monte Carlo method applied to approximating the value of π.
计算定积分
假设我们要求解$f(x)=x^2$在$[0, 2]$间的积分,即下图函数曲线与$x$轴围成的面积
![$f(x)=x^2$在$[0, 2]$间的积分](./x2.png)
其实,求解圆周率其实是在求函数$f(x)=\sqrt{1 - x^2}$在区间$[0, 1]$上的积分。
偶然命中法
像求解圆周率那样,只要求解出一对随机数$(x_i,y_i),x_i\in[0,2],y_i\in[0,4]$落在曲线下方的概率,即可求出$f(x)=x^2$在$[0, 2]$间的积分结果。 $$ H(x, y)=\begin{cases} 1\qquad&if\quad y \le f(x) \\ 0 &else \end{cases}\\ F_n=A \frac{1}{n} \sum^{n}_{i=1} H(x_i,y_i) = h(b-a) \frac{1}{n}\sum^{n}_{i=1} H(x_i,y_i) $$
抽样平均法
还有另外一种蒙特卡罗积分方法是基于计算的平均值理论,即函数的积分结果取决被积函数$f(x)$在$a\le x\le b$的平均值。为了确定这个平均值,用随机的$x_i$来取代规律的$x_i$,抽样平均值方法的积分估计值$F_n$为: $$ F_n=(b-a)\left\lt f\right\gt=\frac{b-a}{n}\sum^n_{i=1}f(x_i) $$
计算高维定积分
高维定积分的解析解 $$ \displaystyle \quad I = \int_{ \Omega } f(\overline{x}) d\overline{x} $$ 其中$\Omega$,是$\mathbb{ R }^m$的子集,拥有体积 $$ \displaystyle \quad V = \int_{ \Omega } d\overline{x} $$ 一般的MC方式是从$\Omega$的均匀分布中获取长度为$N$的随机数序列 $$ \displaystyle \quad \overline{x_1},\overline{x_2},\cdots,\overline{x_N} \in \Omega $$ $N$越大,$I$的值就能被越精确地估计出来 $$ \displaystyle \quad I \approx Q_N \equiv V\left\lt f \right\gt = V \frac{1}{N} \sum^N_{i=1} f(\overline{x_i}) $$ 由于大数法则(Law of large numbers),则 $$ \displaystyle \quad \lim_{N \to \infty} Q_N = I $$ > 高维定积分可参考误差分析
所以用蒙特卡罗方法计算高维定积分是可行
调制随机数(Metropolis–Hastings算法)
在1953年Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, 和 Edward Teller提出了产生任意的非均匀分布的另外一个方法。在1970年被 W. K. Hastings 扩展到更普遍的情况,所以该算法被称作Metropolis–Hastings采样算法。该算法整个过程形成一个马尔科夫链(MCMC)。
我们常见的概率分布,无论是连续还是离散的分布,都可以基于均匀分布的样本来生成。无论是正态分布、指数分布等等,都可以用数学变换来得到。可当$p(x)$的形式很复杂,或者$p(x)$是一个高维的分布的时候,就很难生成符合该分布的样本了。而Metropolis-Hastings采样算法解决了这个问题,给定一个概率分布函数,即可生成符合这一概率分布的样本。
要想明白Metropolis–Hastings采样算法,就想要明白马尔可夫链(Markov Chain)及马尔可夫收敛定理(Markov Convergence Theore)。
马尔可夫链(Markov Chain)
先举个简单的例子,马拉松比赛跑者众多,几万人跑步。假设一万个人一起出发,分为三个梯队,第一梯队1k个人,第二2k个人,第三7k个人。 这三个梯队间的转移概率如下 $$ \begin{array}{c|ccc} 状态 & 第一梯队 & 第二梯队 & 第三梯队 \\ \hline 第一梯队 & 0.65 & 0.30 & 0.05 \\ 第二梯队 & 0.15 & 0.60 & 0.25 \\ 第三梯队 & 0.20 & 0.10 & 0.70 \end{array} $$ 使用矩阵来表示,概率转移矩阵如下: $$ P = \begin{bmatrix} 0.65 & 0.30 & 0.05 \\ 0.15 & 0.60 & 0.25 \\ 0.30 & 0.40 & 0.30 \end{bmatrix} $$
假如这一刻的梯队分布为$\pi_0=\begin{bmatrix}\pi_0(0)&\pi_0(1)&\pi_0(2)\end{bmatrix}$,那么下一刻的分布矩阵将是$\pi_1=\pi_0P$,下下一刻的分布矩阵将是$\pi_2=\pi_1P=\pi_0P^2$,…,第$n$刻的分布矩阵将是$\pi_n=\pi_0P^n$。
初始分布矩阵为$\pi_0=\begin{bmatrix}1.00k&2.00k&7.00k\end{bmatrix}$,则可以计算前n刻的分布情况 $$ \begin{array}{c|ccc} 第n刻 & 第一梯队 & 第二梯队 & 第三梯队 \\ \hline 0 & 1.00k & 2.00k & 7.00k \\ 1 & 3.05k & 4.30k & 2.65k \\ 2 & 3.42k & 4.55k & 2.02k \\ 3 & 3.51k & 4.57k & 1.92k \\ 4 & 3.54k & 4.56k & 1.89k \\ 5 & 3.56k & 4.56k & 1.89k \\ 6 & 3.56k & 4.56k & 1.88k \\ 7 & 3.56k & 4.56k & 1.88k \\ 8 & 3.56k & 4.55k & 1.88k \\ \dots & \dots & \dots & \dots \end{array} $$ 可以发现从第7刻开始,分布矩阵几乎就稳定不变了。这是怎么回事?换个初始分布矩阵$\pi_0=\begin{bmatrix}3.00k&4.00k&3.00k\end{bmatrix}$试试 $$ \begin{array}{c|ccc} 第n刻 & 第一梯队 & 第二梯队 & 第三梯队 \\ \hline 0 & 3.00k & 4.00k & 3.00k \\ 1 & 3.45k & 4.50k & 2.05k \\ 2 & 3.53k & 4.55k & 1.91k \\ 3 & 3.55k & 4.56k & 1.89k \\ 4 & 3.56k & 4.56k & 1.88k \\ 5 & 3.56k & 4.56k & 1.88k \\ 6 & 3.56k & 4.55k & 1.88k \\ \dots & \dots & \dots & \dots \end{array} $$ 这次在第6刻就开始稳定不变了,而且两次给定不同的初始分布矩阵,最终都收敛到概率分布$\pi \times 10k=\begin{bmatrix}0.356&0.455&0.188\end{bmatrix} \times 10k$, 而且第二次收敛的速度更快,这是为什么呢?这说明收敛的行为和初始分布$\pi_0$无关,而与概率转移矩阵$P$决定的。第二次收敛更快是因为初始分布比第一次更接近收敛后的分布矩阵。 $$ P^5 = P^6 = \cdots = P^n= \begin{bmatrix} 0.356 & 0.455 & 0.188 \\ 0.356 & 0.455 & 0.188 \\ 0.356 & 0.455 & 0.188 \end{bmatrix} $$ 显而易见,当$n$足够大时,转移矩阵的每一行都会收敛到$\pi=\begin{bmatrix}0.356 & 0.455 & 0.188\end{bmatrix}$。
马尔可夫收敛定理(Markov Convergence Theore)
如果一个非周期马氏链具有转移概率矩阵$P$,且它的任何两个状态是联通的,那么$\displaystyle \lim_{n\to\infty}P^n_{ij}$存在且与$i$无关,即$\displaystyle \lim_{n\to\infty}P^n_{ij}=\pi(j)$
- $\displaystyle \lim_{n \rightarrow \infty} P^n =\begin{bmatrix} \pi(0) & \pi(1) & \cdots & \pi(j) & \cdots \\ \pi(0) & \pi(1) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi(0) & \pi(1) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix} $
- $\displaystyle \pi(j) = \sum_{i=0}^{\infty}\pi(i)P_{ij}$
- $\pi$是方程$\pi P=\pi$的唯一非负解
其中,$$ \pi = \begin{bmatrix}\pi(0) & \pi(1) & \cdots & \pi(j) & \cdots\end{bmatrix}, \quad \sum_{i=0}^{\infty} \pi_i = 1 $$$\pi$称为马氏链的平稳分布。
所有MCMC(Markov Chain Monte Carlo)方法都是以这个收敛定理作为理论基础的。下列是对定理内容的一些解释说明:
- 该定理中马氏链的状态不要求有限,可以是无穷多个的。
- 两个状态$i,j$是联通的,并非指直接一步即可从$i$转移到$j$($P_{ij}\gt0$),而是值$i$与$j$之间可以通过有限步$n$转移到达($P_{ij}^n\gt0$)。 马氏链的任何两个状态联通是指存在一个$n$,使得$\forall i,\forall j,\quad P^n_{ij} \gt 0$。
我们用$X_i$表示在马氏链上跳转第$i$步后所处的状态,如果$\displaystyle \lim_{n\to\infty}P^n_{ij}=\pi(j)$存在,即可证明以上定理的第二个结论。
$ \begin{align} P(X_{n+1}=j)&=\sum^\infty_{i=0}P(X_n=i)P(X_{n+1}=j\mid X_n=i) \\ &=\sum^\infty_{i=0}P(X_n=i)P_{ij} \end{align} $两边同时对$n$取极限可得,$\displaystyle \pi(j) = \sum_{i=0}^{\infty}\pi(i)P_{ij}$。
可以利用MC的平稳分布,来生成符合某些难以生成的概率分布的随机数。从初始概率分布$\pi_0$出发,每一次在马氏链上做状态转移时,记$X_i$的概率分布为$\pi_i$,则有: $$ \begin{align} &X_0\sim\pi_0(x) \\ &X_i\sim\pi_i(x), \quad \pi_i(x)=\pi_{i-1}(x)P=\pi_0(x)P^n \end{align} $$ 由于马尔可夫收敛定理(Markov Convergence Theore),概率分布$\pi_i(x)$将收敛到平稳分布$\pi(x)$。假设到第$n$的时候马氏链收敛,则有: $$ \begin{align} X_0 & \sim \pi_0(x) \\ X_1 & \sim \pi_1(x) \\ & \cdots \\ X_n & \sim \pi_n(x)=\pi(x) \\ X_{n+1} & \sim \pi(x) \\ X_{n+2}& \sim \pi(x) \\ & \cdots \end{align} $$ 所以$X_n,X_{n+1},X_{n+2},\cdots \sim \pi(x)$都是同分布的随机变量, 当然他们并不独立。如果我们从一个具体的初始状态$x_0$开始,沿着马氏链按照概率转移矩阵做跳转,那么我们得到一个转移序列$x_0, x_1, x_2, \cdots x_n, x_{n+1}\cdots$,由于马氏链的收敛行为,$x_n, x_{n+1},\cdots$都将是平稳分布$\pi(x)$的样本。
Metropolis-Hastings采样算法
结合蒙特卡罗方法,构造概率转移矩阵,使得马尔可夫链的平稳分布恰好符合我们想要的分布$P(x)$。这个方式被称作马尔科夫蒙特卡洛(MCMC|Markov Chain Monte Carlo)方法,而Metropolis-Hastings采样算法为其中的一种常用的改进算法。
如果非周期马氏链的转移矩阵$P$和分布$\pi(x)$满足 $$ \pi(i)P_{ij}=\pi(j)P_{ji},\quad \forall i,\forall j \tag{一}\label{0} $$ 则$\pi(x)$是马氏链的平稳分布,上式被称为细致平稳条件(detailed balance condition)。
其实这个定理是显而易见的,因为细致平稳条件$\eqref{0}$的物理含义就是,对于任何两个状态$i,j$,从$i$转移出去到$j$而丢失的的概率质量,恰好会被从$j$转移回$i$的概率质量补充回来,所以状态$i$上的概率质量$\pi(i)$是稳定的,即$\pi(x)$是马氏链的平稳分布。
由细致平稳条件$\eqref{0}$可得 $$ \begin{align} & \sum_{i=1}^\infty \pi(i)P_{ij} = \sum_{i=1}^\infty \pi(j)P_{ji} = \pi(j) \sum_{i=1}^\infty P_{ji} = \pi(j) \\ \implies \quad &\pi P = \pi \end{align} $$ 由于$\pi$是方程$\pi P=\pi$的解,所以$\pi$是平稳分布。
假设我们已经有一个转移矩阵为$Q$的马氏链,显然未收敛时,有 $$ p(i)q(i,j)\neq p(j)q(j,i) $$ 其中$q(i,j)$表示从状态$i$转移到状态$j$的概率,也可写作$q(j|i)$或者$q(i\to j)$。 上式不满足细致平稳条件$\eqref{0}$,所以$p(x)$不可能是这个马氏链的平稳分布。如果我们对马氏链进行改造,使得细致平稳条件$\eqref{0}$成立?尝试引入一个$\alpha(i,j)$,使得两边相等 $$ p(i)q(i,j)\alpha(i,j)=p(j)q(j,i)\alpha(j,i) \tag{二}\label{1} $$ 我们称$\alpha(i,j)$为接受率,按照对称性,得 $$ \alpha(i,j)= p(j) q(j,i) \\ \alpha(j,i) = p(i) q(i,j) $$ 所以$\eqref{1}$就成立了,所以有 $$ p(i) \underbrace{q(i,j)\alpha(i,j)}_{Q'(i,j)} = p(j) \underbrace{q(j,i)\alpha(j,i)}_{Q'(j,i)} \tag{三}\label{2} $$ 这样就把原来的转移矩阵$Q$的马氏链,改造成一个具有新的转移矩阵$Q’$的马氏链,而$Q’$恰好满足细致平稳条件$\eqref{0}$,这样$p(x)$就是这个马氏链$Q’$的平稳分布。 $$ \require{AMScd} \begin{CD} \cdots @>>> x_i @>q(i,j)>> x_j @>>> \cdots \\ \\ @. \begin{matrix}1-\alpha(i,j) \\ 拒绝转移\end{matrix} @. \begin{matrix}\alpha(i,j) \\ 接受转移\end{matrix} \end{CD} $$ 接受率可以这么理解,当马氏链从状态$i$以$q(i,j)$的概率跳转到状态$j$时,以$\alpha(i,j)$的概率去接受这个转移,那么马氏链新的转移概率为两者的乘积$q(i,j)\alpha(i,j)$。
假设我们已经拥有了一个转移矩阵$Q$,把上面的过程整理一下,我们就得到了如下的用于产生符合概率分布$p(x)$的随机数算法。 $$ \begin{array}{l} MCMC 采样算法 \\ \hline 1. 初始化马氏链初始状态X_0=x_0 \\ 2. 对于t=0,1,2,\cdots,循环以下过程进行采样 \\ \qquad \bullet \quad 第t个时刻马氏链状态为X_t=x_t,采样y\sim q(x,x_t) \\ \qquad \bullet \quad 从均匀分布采样u\sim Uniform(0,1) \\ \qquad \bullet \quad 如果u \lt \alpha(x_t,y) = p(y)q(x_t,y)则接受转移x_t \to y,即X_{t+1} = y \\ \qquad \bullet \quad 否则不接受转移,即X_{t+1}=x_t \\ \end{array} $$ 上述过程中$p(x)$,$q(x,y)$说的都是离散的情况,实际上即便是连续的,以上算法仍然有效。
以上MCMC采样算法还有个小问题,转移过程中若是$\alpha(i,j)$偏小(毕竟是两个分布$p(x)$和$q(x,y)$的乘积),而$u \sim Uniform(0,1)$难以小于$\alpha(i,j)$,这样算法过程中马氏链容易原地踏步,拒绝大量转移,这使得收敛到平稳分布$p(x)$的速度太慢。那如何提高接受率,加快收敛速度?
假设$\alpha(i,j)=0.1,\alpha(j,i)=0.2$,此时满足细致平稳条件$\eqref{0}$,于是 $$ p(i)q(i,j)\times 0.1 = p(j)q(j,i) \times 0.2 $$ 上式两边同时扩大5倍 $$ p(i)q(i,j)\times 0.5 = p(j)q(j,i) \times 1 $$ 这样我们把$\alpha(j,i)$提高到$1$,那么从状态$i$到$j$必然会转移,而且细致平稳条件$\eqref{0}$没有被打破!这启发我们可以把细致平稳条件$\eqref{2}$式中的$\alpha(i,j)$,$\alpha(j,i)$同比例放大,使得两者中最大一个放大到$1$,这样我们就提高了算法中转移的接受率,加快收敛速度。 $$ \alpha(i,j) = \min \left\{ \frac{p(j)q(j,i)}{p(i)q(i,j)} , 1 \right\} $$ 于是对上述MCMC采样算法改造,我们就得到了Metropolis-Hastings算法 $$ \begin{array}{l} \text{Metropolis-Hastings 采样算法} \\ \hline 1. 初始化马氏链初始状态X_0=x_0 \\ 2. 对于t=0,1,2,\cdots,循环以下过程进行采样 \\ \qquad \bullet \quad 第t个时刻马氏链状态为X_t=x_t,采样y\sim q(x,x_t) \\ \qquad \bullet \quad 从均匀分布采样u\sim Uniform(0,1) \\ \qquad \bullet \quad 如果u \lt \alpha(x_t,y) = \min\left\{\frac{p(j)q(j,i)}{p(i)q(i,j)},1\right\}则接受转移x_t \to y,即X_{t+1} = y \\ \qquad \bullet \quad 否则不接受转移,即X_{t+1}=x_t \\ \end{array} $$
误差分析
蒙特卡罗方法,只是用随机数来解决很多问题的方法统称。无法提出一个对所有蒙特卡罗方法进行误差分析的方法,只能具体问题具体分析。
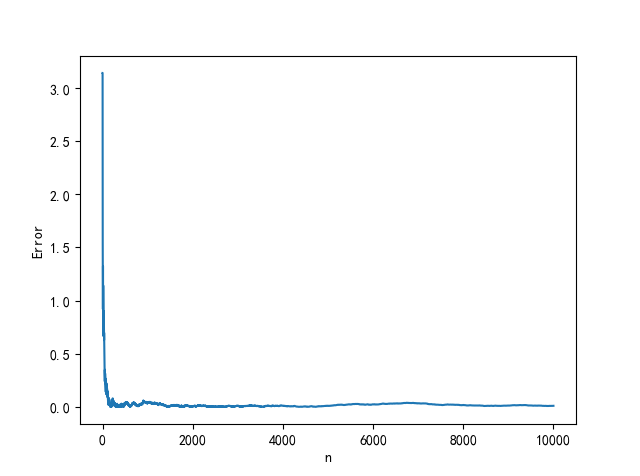
比如用MC方法求解$\pi$的数值,用计算定积分的方式计算,也就是计算函数$f(x)=\sqrt{1 - x^2}$在区间$[0, 1]$上的积分。对于一次实验产生的$10^4$随机数的序列,用抽样平均法$\displaystyle F_N=V \frac{1}{N} \sum ^N _{i=1} f(x_i)=V\left\lt f \right\gt$可得$F_N=3.1489$。与准确结果比较,可以发现,这次试验结果误差大约是$0.0073$。
当然这只是一次实验的误差,没有什么说服力,若是计算随机数序列整体结果的方差 $$ \operatorname{Var}(f)=\sigma_N^2 = \left\lt f^2 \right\gt - \left\lt f \right\gt^2 \\ 其中,\left\lt f \right\gt = \frac{1}{N}\sum^N_{i=1}f(x_i),\left\lt f^2 \right\gt = \frac{1}{N}\sum^N_{i=1}f^2(x_i) $$ 那么积分结果的方差为: $$ \operatorname{Var}(F)=\sigma^2= \frac{V^2}{N^2} \sum ^N _{i=1} \operatorname{Var}(f)=V^2 \frac{\sigma_N^2}{N} $$ 按照上式计算,结果如下方左图所示 $$ \begin{array}{c|ccc} n & \sigma & \sigma_N & F_N & | F_n - \pi | \\ \hline 10^1 & 1.0407 \times 10^{-1} & 8.2278 \times 10^{-2} & 3.339699 & 0.198106 \\ 10^2 & 1.7298 \times 10^{-2} & 4.3244 \times 10^{-2} & 3.190591 & 0.048999 \\ 10^3 & 2.0576 \times 10^{-3} & 1.6267 \times 10^{-2} & 3.175076 & 0.033483 \\ 10^4 & 2.2095 \times 10^{-4} & 5.5236 \times 10^{-3} & 3.155933 & 0.014341 \\ 10^5 & 2.5398 \times 10^{-5} & 2.0079 \times 10^{-3} & 3.145450 & 0.003858 \\ 10^6 & 3.4241 \times 10^{-6} & 8.5602 \times 10^{-4} & 3.142984 & 0.001391 \\ 10^7 & 4.9500 \times 10^{-7} & 3.9133 \times 10^{-4} & 3.141403 & 0.000189 \\ 10^8 & 5.0821 \times 10^{-8} & 1.2705 \times 10^{-4} & 3.141461 & 0.000132 \\ 10^9 & 5.0482 \times 10^{-9} & 3.9909 \times 10^{-5} & 3.141595 & 0.000002 \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{array} $$
可以很明显地看出,$\sigma$随着$N$的增大而减少。除了一味的增加$N$来降低误差,还有别的什么方法吗?接下来讲的两种方法从一定程度上降低了误差。
递归分层抽样(Recursive stratified sampling)
递归分层抽样过程的是:在每个递归步骤中,使用普通蒙特卡罗算法估计积分和误差。当如果误差估计大于所需精度,则其积分区域被分割为子集,并且把算法重新应用于子集中。 分层采样算法将采样点集中在函数方差最大的区域,从而减小大差异,使抽样更有效。该思路最热门的实现是MISER算法。
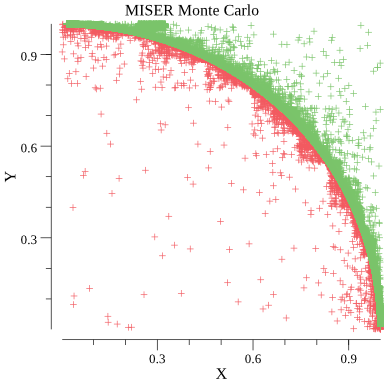
上图是用MISER算法求解$\pi$的采样点分布图。可以看出采样点形成了弧状轮廓。 $$ H(x, y)=\begin{cases}1, \quad &if\ x^2+y^2 \le 1 \\0, &else \end{cases}\quad x,y\in [0,1) \\ F_n=A \frac{1}{n} \sum^{n}_{i=1} H(x_i,y_i) = \frac{1}{n}\sum^{n}_{i=1} H(x_i,y_i) $$ 这是因为在曲线$y=\sqrt{1-x^2}$附近是方差最大的区域,所以采样点几乎都集中在此曲线附近。 $$ \begin{array}{c|cccc} n & n_{Real} & \sigma & \sigma_N & F_N & | F_n - \pi | \\ \hline 10^{3} & 523 & 5.1189 \times 10^{-3} & 4.0468 \times 10^{-2} & 3.195360 & 0.053767 \\ 10^{4} & 2757 & 2.2615 \times 10^{-4} & 5.6537 \times 10^{-3} & 3.140075 & 0.001518 \\ 10^{5} & 15964 & 1.2168 \times 10^{-5} & 9.6193 \times 10^{-4} & 3.140571 & 0.001022 \\ 10^{6} & 92098 & 2.2333 \times 10^{-7} & 5.5832 \times 10^{-5} & 3.141635 & 0.000042 \\ 10^{7} & 522175 & 7.3403 \times 10^{-8} & 5.8030 \times 10^{-5} & 3.141666 & 0.000073 \\ 10^{8} & 2969563 & 3.7979 \times 10^{-10} & 9.4949 \times 10^{-7} & 3.141599 & 0.000006 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array} $$
对比之前获得的结果,发现MISER算法能用更少的采样点获取到更小的$\sigma$。这样既提高了精度,又减少了所需要的计算时间。
代码 Gist | Monte Carlo method applied to approximating the value of π.
重要抽样法(Importance sampling)
重要抽样法是一个能很好地提高蒙特卡罗积分算法精度的方法,即减少方差$\sigma^2$值。 做法是,在积分函数中引入一个整函数$p(x)$,则其应满足 $$ \int^b_{b} p(x)dx = 1 $$ 那么积分函数转变成 $$ I = \int^a_{b}\left[\frac{f(x)}{p(x)}\right]p(x)dx $$ 那么积分的估计值$F_n$为 $$ F_n=\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x_i)} $$ 对于均匀分布的情况 $p(x)=\frac{1}{b-a}$
$$ F_n=\frac{b-a}{n}\sum^n_{i=1}f(x_i) $$这就是一般的蒙特卡罗积分方式,而我们的目的是选择一个$p(x)$使得被积分函数$\frac{f(x)}{p(x)}$的方差最小。 比如,我们要求$\displaystyle \int^1_0 e^{-x^2} dx$,比较合理的选择是$p(x)=Ae^{-x}$,其中$A$为归一化常数。
$$ \begin{array}{ccc} p(x)=\frac{1}{b-a}=1 & \quad & p(x)=Ae^{-x} \\ \begin{array}{c|cc} n & \sigma & \sigma_N \\ \hline 10^{1} & 3.6575 \times 10^{-2} & 1.1566 \times 10^{-1} \\ 10^{2} & 4.0660 \times 10^{-3} & 4.0660 \times 10^{-2} \\ 10^{3} & 4.4666 \times 10^{-4} & 1.4125 \times 10^{-2} \\ 10^{4} & 4.6555 \times 10^{-5} & 4.6555 \times 10^{-3} \\ 10^{5} & 7.1814 \times 10^{-6} & 2.2710 \times 10^{-3} \\ 10^{6} & 1.0165 \times 10^{-6} & 1.0165 \times 10^{-3} \\ 10^{7} & 1.0675 \times 10^{-7} & 3.3759 \times 10^{-4} \\ 10^{8} & 1.1489 \times 10^{-8} & 1.1489 \times 10^{-4} \\ 10^{9} & 1.1608 \times 10^{-9} & 3.6709 \times 10^{-5} \\ \cdots & \cdots & \cdots \end{array} & \quad & \begin{array}{c|cc} n & \sigma & \sigma_N \\ \hline 10^{1} & 7.4557 \times 10^{-3} & 2.3577 \times 10^{-2} \\ 10^{2} & 1.0579 \times 10^{-3} & 1.0579 \times 10^{-2} \\ 10^{3} & 1.1004 \times 10^{-4} & 3.4796 \times 10^{-3} \\ 10^{4} & 1.1655 \times 10^{-5} & 1.1655 \times 10^{-3} \\ 10^{5} & 1.4812 \times 10^{-6} & 4.6840 \times 10^{-4} \\ 10^{6} & 1.6222 \times 10^{-7} & 1.6222 \times 10^{-4} \\ 10^{7} & 1.7185 \times 10^{-8} & 5.4343 \times 10^{-5} \\ 10^{8} & 1.9564 \times 10^{-9} & 1.9564 \times 10^{-5} \\ 10^{9} & 9.7523 \times 10^{-10} & 3.0840 \times 10^{-5} \\ \cdots & \cdots & \cdots \end{array} \end{array} $$虽然使用非均匀分布$p(x)$加大计算消耗,但提高了精度。在实际使用中要权衡二者,再考虑是否使用。
蒙特卡洛方法的其它应用
最近柯洁对战AlphaGo输了,人类在围棋上终究输给了机器。有点小难过,可能我是人类吧 :) AlphaGo的背后就是使用了蒙特卡洛树搜索(英语:Monte Carlo tree search;简称:MCTS)和深度学习。蒙特卡洛树搜索也被用于其他棋盘游戏程序,如六贯棋、三宝棋、亚马逊棋和印度斗兽棋;即时电子游戏,如《吃豆小姐》、《神鬼寓言:传奇》、《罗马II:全面战争》;不确定性游戏,如斯卡特、扑克、万智牌、卡坦岛。
最后用miser画了个蝙蝠镖的图,哈哈真好看
参考
- What is Monte Carlo? | YouTube
- Monte Carlo method | Wikipedia
- Monte Carlo integration | Wikipedia
- Metropolis–Hastings algorithm | Wikipedia
- LDA-math-MCMC 和 Gibbs Sampling | 统计之都
- Rickjin靳志辉,LDA数学八卦,0.4 MCMC⁄Gibbs Sampling
- Recursive Stratified Sampling | WilliamH, Press. NUMERICAL RECIPES-The Art of Scientific Computing Third Edition[M]. Cambridge:Cambridge University Press, 2007. 323-328
- 蒙特卡洛树搜索 | Wikipedia







